前回、麻雀の手作りではブロック数を把握することで簡単にいらない牌を見分けることができると書きました。
(記事リンク)
今回は手牌のブロック数が4つ以下の場合の考え方を解説します。
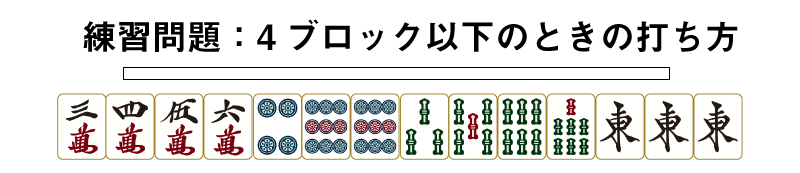
例としてはこんな手牌です。

この手牌をブロックにわけると

となりますからブロック(=メンツ・雀頭・その候補となる部分)は4つ、さらにまだブロックではない孤立牌が3枚です。
おさらいとなりますが麻雀は4メンツ1雀頭を作るとアガリとなるゲーム(七対子と国士無双を除く)であり、これはすなわち5ブロックを目指すゲームということです。
4ブロック以下の手牌というのは、目標である5ブロックに対して1ブロック足りないため孤立牌の中からブロックになりやすい牌を残していくことになります。
孤立牌を「ブロックになりやすさ」でランキングしたものが次の表です。自分の手牌が4ブロック以下の場合はこのランキングで最も順位の低い牌を切るのが正解となります。
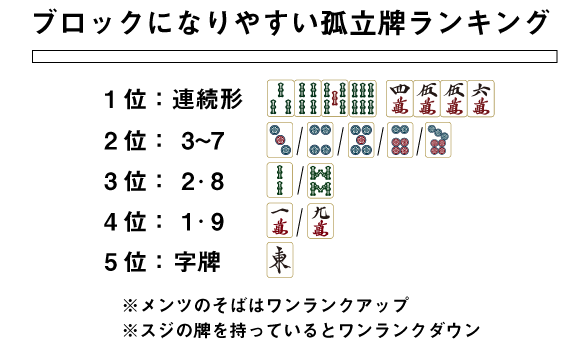
2位〜5位については「受け入れ枚数の基本」で解説した通りですので今回は割愛します。
(記事リンク)
そのほかの部分について解説していきましょう。
1位:連続形
連続形とは、簡単に言えば麻雀牌が何枚も(普通は4枚以上)くっついている形を指します。麻雀は牌がくっつけばくっつくほど受け入れが増える性質があるのです。チンイツの待ちがわけわからない!という経験をしたことがある方は多いと思いますが、それと同じ理屈です。
連続形の中でも特に重要な形を紹介します。これは必ず覚えてください。
①四連形
2345mや34567pといった牌が4つ並んだ形を四連形といいます。
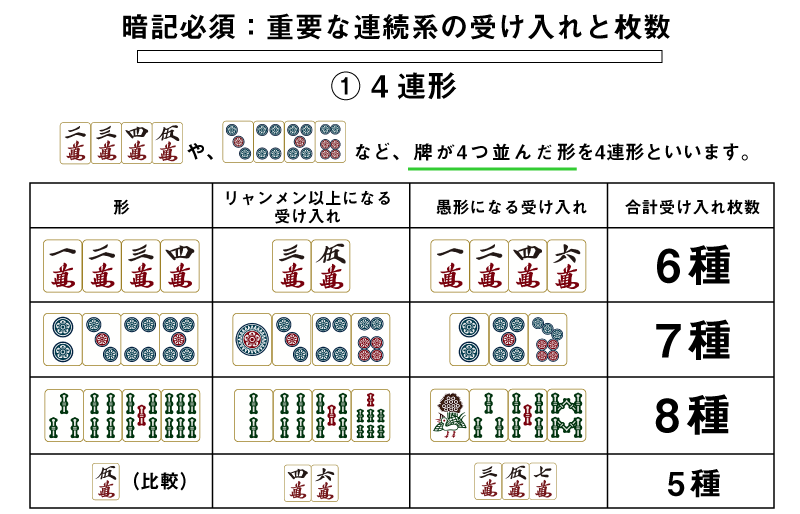
このように、四連形は孤立牌と比べて圧倒的に受け入れ枚数が多くなるため、4ブロック以下の手牌では最優先で残すべき形です。
1234mや6789sのような端にかかる四連形はそこまでではありませんが、真ん中に近い四連形は受け入れ枚数そのものが多いだけでなく、23456pや34567sのような3メンチャンになる可能性がある非常に強い形です。
間違っても「1メンツ確定しているから」などと言って切らないようにしましょう。
②中ぶくれ
次に3445mや6778sのように、メンツの真ん中の牌だけが2枚ある形について解説します。これを「中ぶくれ」と呼びます。
今回も表にして受け入れ枚数を比べてみましょう。
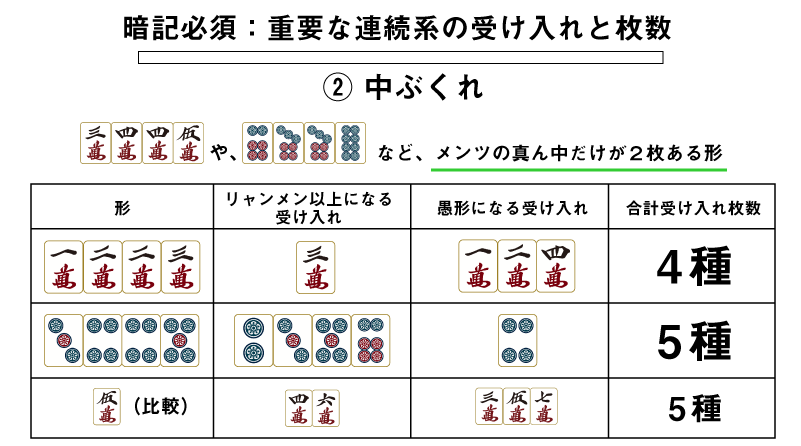
合計の受け入れ枚数だけ数えると、実は中ぶくれは孤立牌とは差がありません。
ではなぜ中ぶくれが優秀な形かというと、リャンメン待ちを作りやすいからです。
孤立の5mがリャンメンになるためには4mか6mを引いてこなければいけませんが、
4556mという形であれば3467mのどれを引いてもリャンメン待ちができます。
このように、この瞬間の受け入れ枚数は変わらない(厳密には自分が使っている分少し少ない)もののリャンメン待ちという良い形ができやすい分、早くテンパイしたりテンパイしたとにアガリやすかったりするため「良い形」と言えるのです。
四連形と並んでこの中ぶくれも4ブロック以下の手牌では積極的に残すべきであると言えます。
ここから次の区切りまで平澤に確認
※メンツのそばはワンランクアップ
1位:連続形
2位:3〜7牌
3位:2・8牌
4位:1・9牌
5位:字牌
※メンツのそばはワンランクアップ
※スジの牌を持っているとワンランクダウン
次は欄外に補足としていれた2項目について解説します。まずは「メンツのそばはワンランクアップ」についてです。

例えばこんな形です。3456sの部分は四連形ですから残すとして1mと1pを比較することになります。
シンプルに考えればどちらもランキング4位の「1・9牌」ですから差はないように見えますが実は差があります。
マンズの1345mに、6mを引いた時のことを考えてみましょう。
13456mという形になりカン2m待ちのブロックができました。
もしくは2mを引いた形を考えてみます。
12345mという形になりリャンメン待ちとなりました。
ピンズは2pを引いたところで12456pですからペンチャン待ちです。
このように1mの近く(ひとつ飛ばして隣)に345mというメンツがあることで、6mの受け入れが増え、2m引きでリャンメンになるという風にパワーアップしました。
これは孤立の1pと比べると明確にブロックになりやすいといえますから「ワンランクアップ」なのです。
※筋の牌を持っちるとワンランクダウン
1位:連続形
2位:3〜7牌
3位:2・8牌
4位:1・9牌
5位:字牌
※メンツのそばはワンランクアップ
※スジの牌を持っているとワンランクダウン
次はもう1つの補足事項「スジの牌を持っているとワンランクダウン」について解説します。

こんな形から何を切るか、という問題ですが今回も1mに着目してみましょう。
通常1mと中を比べれば1mの法が受け入れが多い、すなわちブロックになりやすいものです。
中は中そのものをツモらなければブロック化しないのに対して1mは1m以外にも2mや3mでも良いからです。
しかし今回の手の中に1mの「スジ」にあたる4mがあります。
スジがわからない方はこちらの記事を参照
(記事リンク)
もし仮に2mを切ったとしても
2mツモ→24m
3mツモ→34m
というように新たにブロックができます。
すなわち1mの役割を4mが奪ってしまっているのです。
1mだけの受け入れは1mツモのみ、それなら枚数は中しかかわりません。今回はポンして役ができる分中の法が優れていると言えそうです。
このようにスジの牌を持っている場合は、受け入れとなる牌が重複するのでブロックになりやすさという意味においては価値が低下します。したがって「ワンランクダウン」です。
では練習問題をやってみましょう。次のランキングをじっくり見ながら考えてみてください。

まずこの手牌をブロックにわけてみましょう

孤立牌はカッコでくくっています。
ブロックとなっているのは4つですから、カッコ内の孤立牌を比較してもっともランキングの低い牌を切ります。
まず6mは3456mという「四連形」ですからランキング1位です。優先的に残しましょう。
ということで残るは4pと3sの選択です。
一見するとどちらもランキング2位の3~7牌ですが、ソーズは567sがあります。これは「メンツのそばはワンランクアップ」に該当しますから、実質1位相当(厳密には四連形の法が強いですがわかりやすさ重視ということでお許しください)。
したがって単独2位の4pがランキング最下位。ここで切るのは4pが正解です。
いかがでしたでしょうか。
大抵の手牌は最初は4ブロック以下ではじまりますから、この孤立牌の比較は非常に重要となります。
今回の記事が少し難しかったという方はこちらの記事も参考にしてみてください。
(受け入れ枚数を知る 記事リンク)






この記事へのコメントはありません。